こんにちは、おーです!
友人と共有したい「お金の話シリーズ」の続きです。
先日投稿したブログ記事「貯蓄:銀行預金」でも簡単にふれましたが、「単利」と「複利」についてざっくりとではありますが、自分の感想も含めてまとめておきたいと思います。
(関連記事は本記事の一番下にリンクを貼っています、興味のある方はよろしければそちらからご参照をお願いします)
あくまで個人の学びをもとにした参考記事となります。予めご了承をお願いします。
私の結論:複利の力を知らない、知っていても活用しないのは「非常にもったいない!!」です。
お金の運用を考える際「金利」は気にしますが、それに加えて「単利」と「複利」のどちらで運用するのかもあわせて検討することが、非常に重要であることに気付けました。
人生の有限な時間の中で、私たち自身の労働力とは別に「いかにお金にも働いてもらうか」、「いかに効率的に運用していくか」を考えるためにも非常に重要な知識だと改めて思いました。
「単利」と「複利」の違い
「単利」と「複利」という言葉をすでにご存知の方、なんとなく聞いたことがある方も多いと思います。
そして知っている方は口を揃えて「複利はスゴい!」とおっしゃいます(というのは私の個人的感想ですが、あながち間違いではないと思います)。
何がそんなにスゴいのか?言葉ではなかなかイメージが伝わりにくいと思いますので、違いを知るために、まずは「単利」と「複利」の違いを試算してみたいと思います。
条件は以下とします。
| 預入額 | 100万円(初期に預けてそのまま放置、追加入金なし) |
|---|---|
| 運用期間 | 1年~40年 |
| 運用方法 | 「単利」と「複利」 |
| 金利 | 5%で試算 |
| 税金 | 本試算においては考慮しない(実際、受取時に約20%の課税あり) |
注:金利0.200%(2020年9月現在の定期預金の金利)から得られる複利の効果は小さいため、省略します。
なお、気になる方は下でご紹介する電卓での複利計算方法で算出してみていただくと比較として参考になると思います(批判するものではありませんが、現在の定期預金金利などではいかに資産が殖えにくいか、という意味でです)。
【試算】100万円を「単利」と「複利」でそれぞれ運用
単利の場合
元本は100万円のまま変わらない(=元本は増えない)
利息額も毎年一律、一定で変わらない(=元本が増えないから)
「単利」とは区切られた時期(この場合1年)で一度区切り、改めて次の1年をスタートを繰り返すイメージ
複利の場合
元本は前年の利息が加算されて徐々に増えていく
元本に前年の利息が加算されることでさらに利息額も徐々に増えていく
「複利」とは時間の経過とともに雪だるま式に積み重なっていくイメージで長期になればなるほど効果が大きくなる
注:実際の受取時には税金が控除されます
上記のポイントをもとに、下の試算結果と推移グラフをみていただければと思います。
(試算結果)
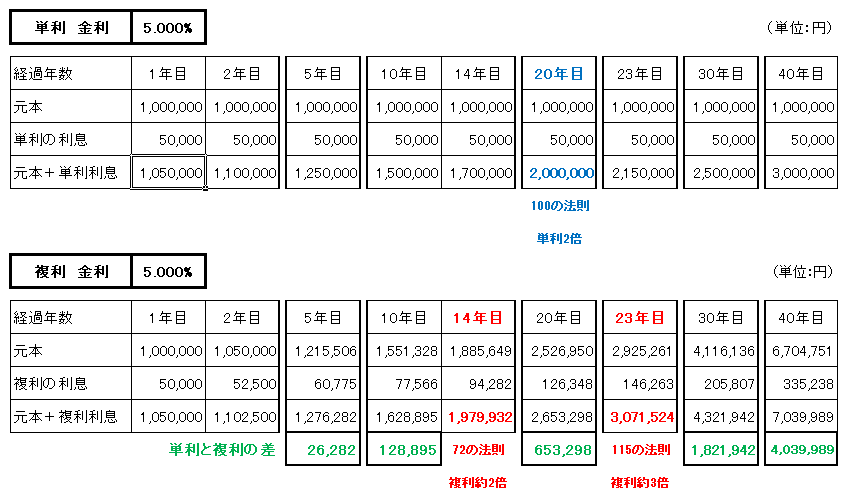
上の試算結果をもとにグラフを作りました。
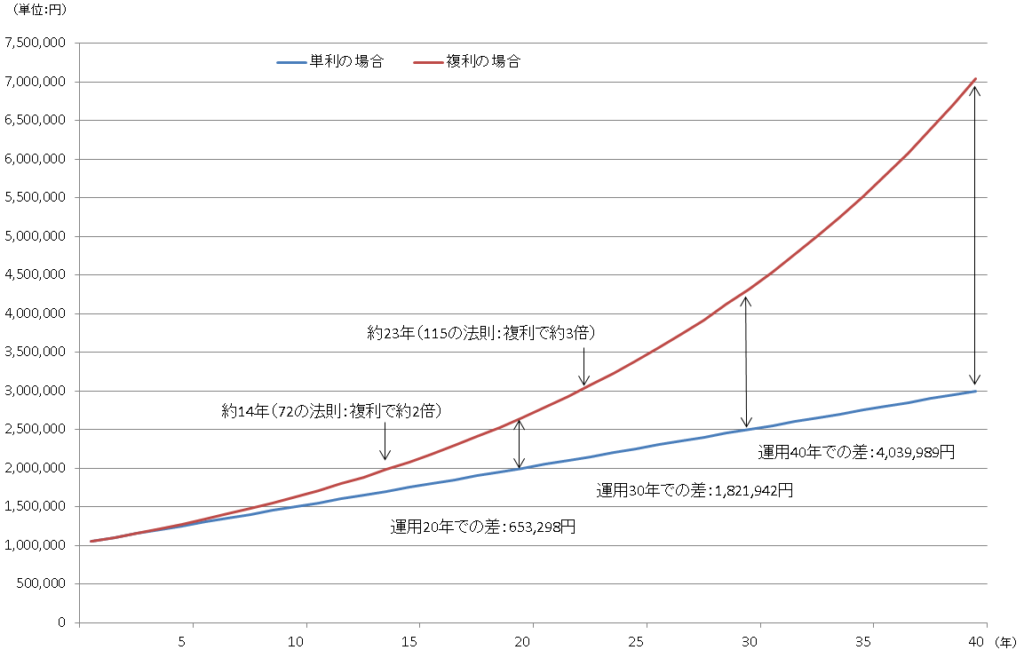
下のグラフは100万円を最長40年(20歳から60歳までと仮の想定)で運用した場合の資産推移を示したグラフです。
注意事項:元本が維持され、かつ安定して理想的に複利が働いた場合をイメージした、あくまで理想的な試算で、実際このように毎年増えるとは限りません、ご注意をお願いします。
(推移グラフ)
参考:72の法則、100の法則、115の法則
上記計算結果とグラフでもそれぞれ表示していますが、今回のケースであれば以下のとおりです。
単利で2倍=100の法則 100 ÷ 5 ≒ 預けているお金が2倍になるまで20年
複利で2倍=72の法則 72 ÷ 5 ≒ 預けているお金が2倍になるまで約14年
複利で3倍=115の法則 115 ÷ 5 ≒ 預けているお金が3倍になるまで約23年
72の法則
金利を利用して資産を2倍にするために必要な「年数」を計算する。72を予定運用利回りで割ることで「”複利”でおおよそ何年後に現在の資産が2倍になるか」を求める。
72 ÷ 金利 ≒ 預けているお金が2倍になるまでの年数(概算値)
100の法則
上記の考え方と同じように「”単利”でおおよそ何年後に現在の資産が2倍になるか」を求める。
100 ÷ 金利 ≒ 預けているお金が2倍になるまでの年数(概算値)
115の法則
考え方は同様で「金利を利用して”複利”でおおよそ何年後に現在の資産が3倍になるか」を求める。
115 ÷ 金利 ≒ 預けているお金が3倍になるまでの年数(概算値)
参考:複利を電卓で計算する方法
参考に電卓でポチポチ計算する方法も掲載しておきます。
本記事では掲載していませんが、現在の金利0.200%でも計算されてみてはいかがでしょうか。
(1年単位で利息計算されると仮定しています)
| A.計算したい金利を基準とする | 例1 0.200% | 例2 5% |
| B. 計算したい金利を100で割る | 0.200÷100=0.002 | 5÷100=0.05 |
| C.元金の意味で1を足す | 1+0.002=1.002 | 1+0.05=1.05 |
| D.Cの数値を打ち込み✕を2回押す | ✕ ✕ | あとは左と同じ |
| E.元本金額を入れる(例:100万円) | 1,000,000 | あとは左と同じ |
上記E.のあとは、イコール「=」キーを計算した年数分、繰り返し押していくと、計算結果が複利で増えていき、数値が徐々に大きくなります。
(感想)知らないと損している知識
複利は知らないと損している知識の筆頭ともいえるのでは
お金のことを学ばずにきた私は、別の記事でも述べましたが、このような知識を自ら学びに行くまで知ることもありませんでした。
なかには私のように歳をかさねるまで学ぶ機会やタイミングを逸したまま過ごしておられる方も多いのではないでしょうか。
このような知識を教える場の少ない日本において、もし今日の記事がなんらかの参考になっていれば嬉しく思います。
【2020年10月13日追記】以下の記事で紹介しています「投資信託」という商品は長期で運用することで複利を最大限に活用することができる優秀な商品だと考えています。
元本保証などありませんので、投資は全て自己責任という前提です。
知識や経験にも複利は働くといえるのではないか
お金の話に限らず、知識や経験もゼロをイチに、イチをニに・・・と加算していくことができますね。
こうやって得られた学びや経験が積もりに積もれば、それが自身の将来に渡って長くずっと効かせられる最大の複利効果ではないでしょうか。
知識は奪われません
学ぼうという気持ちで学んだ知識は糧になりますし、きっと何かの役に立つと思います。
こういった繰り返しが長い目でみると大きな差になるということを歳をとってから痛感しております。
お金に働いてもらう投資だけではなく、自分を高める自己投資にも取り組んで、学ぶ姿勢をこれからも大切にしていきたいと思います。
この記事がご参考になれば幸いです。
それではまたっ!!
関連記事です。
本記事の内容は先日投稿した記事「r>gの話」とも絡めて整理しておいたほうがいいかと思います。













